[最新] 球 体積 求め方 917241-球 体積 表面積 求め方
球の体積の求め方 公式の覚え方を語呂合わせで覚えよう 中学数学 テラコヤプラス By Ameba
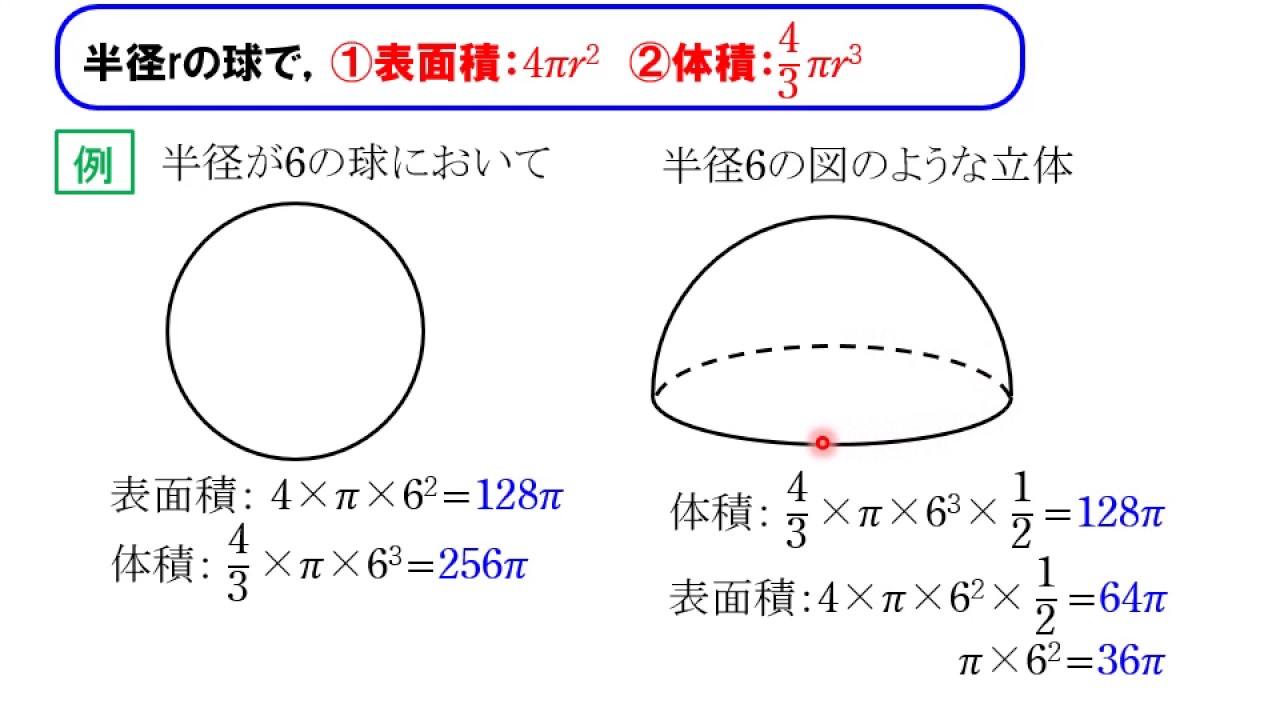
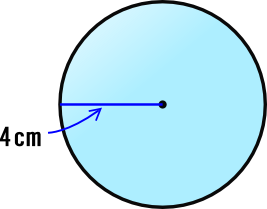
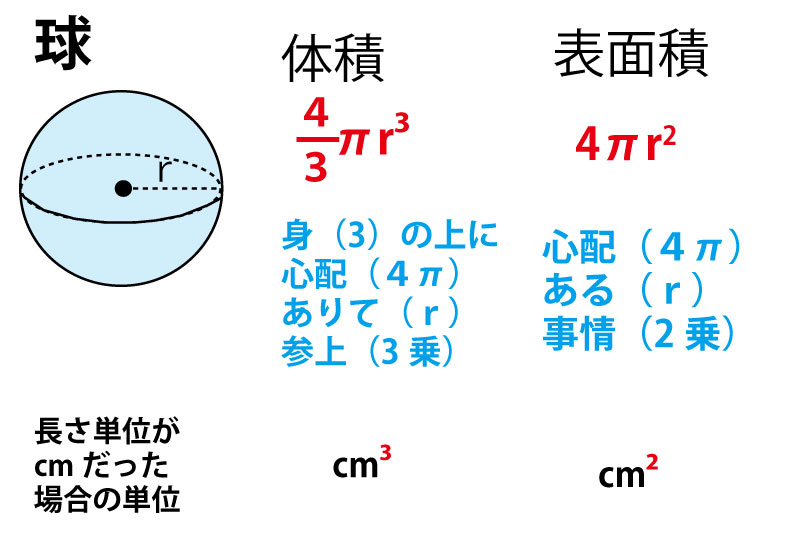
3分の4の理屈は中学校の場合 同じ直径2rと高さ2rを持つ円柱と比べると 体積比が球2対円柱3になるから円柱に対して球の体積は3分の2 円柱の体積=πr二乗×2r=2πr三乗 球=円柱の体積(2πr三乗)×3分の2 =3分の4πr三乗半径4cmの球の表面積と体積を求めよ。 球の表面積は「心配ある事情( 4πr2 4 π r 2 )」より、 4× π× 42 =64π 4 × π × 4 2 = 64 π 球の体積は「身の上に心配あるので参上( 4 3πr3 4 3 π r 3 )」より、 4 3 × π× 43 =256 3 π 4 3 × π × 4 3 = 256 3 π 表面積は 64πcm2 64 π c m 2 、体積は 256 3 πcm3 256 3 π c m 3 ちなみに球の表面積や体積について、自由に印刷できる練習問題を用意
球 体積 表面積 求め方
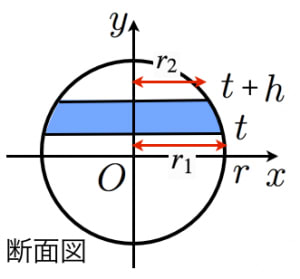
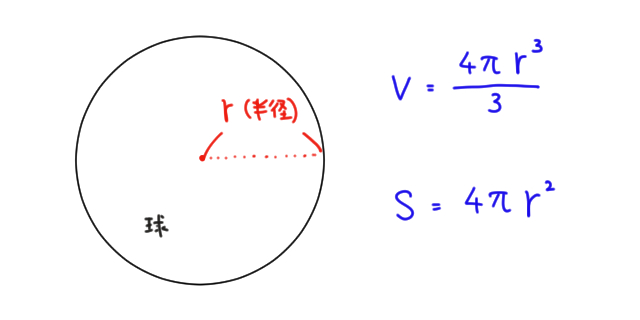
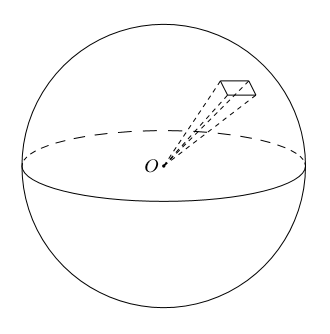
球 体積 表面積 求め方- よって、\(\Delta t\) を限りなく \(0\) に近づけると、球殻の体積について以下の式が成り立つ。 \(\displaystyle \int_0^r S(t) \, dt = \frac{4}{3} \pi r^3\) 上記式において、両辺を \(r\) で微分す 球の体積の公式: V=4/3πr³ 球の体積の公式がなぜこうなるのかという点に関しては、中学数学の範囲で証明することはできません。 しかし、この半径rの球がぴったりおさまる円柱と体積を比べたとき、その比は「 球円柱=23 」となることを覚えておきましょう。 球の体積がイメージしやすくなり、公式を忘れたときにも役立ちます。 「半径rの球がぴったり
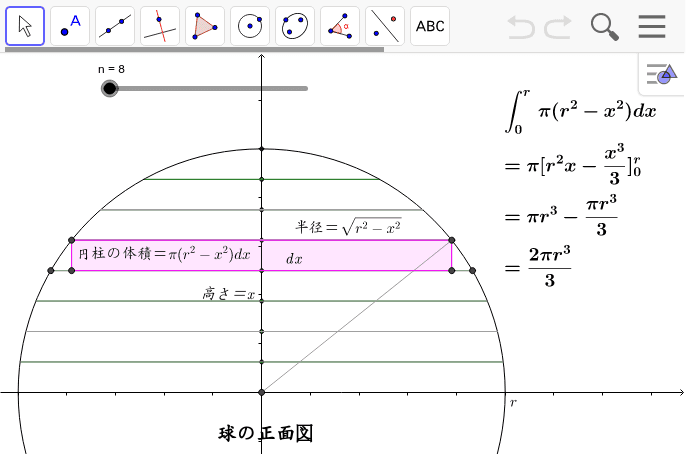
球の体積の求め方とその証明 高等学校で学ぶ積分の知識が必要
球の体積の求め方 半径rの球の体積を求める公式は、次のようになります。 πは円周率(=)です。 球の体積は、半径rの3乗に比例していくということですね! (例題) 半径5cmの球の体積は? 公式にr=5を代入して球の体積の求め方 公式と計算例 Scipursuit 体積の求め方 球 球の体積を求める公式は、次の通りです。 V = 4 3πr3 V = 4 3 π r 3 ここで、V は球の体積、r は球の半径、π は円周率を表します。 球の体積を求めるには、この公式に球の半径 r を代入すればよいだけです。 このページの続きでは、例題を使って、この公式の使い方を説明しています。この四角錐を使って、球を作れば、球の 体積 は、以下になります。 球の 体積 = Δ Sh Δ Sh 以下のように整理します。 = (Δ S Δ S ) h ここで、 Δ S Δ S は、 球の表面積 なので、 4 πh 2 となります。 = πh 3 h は、球における半径なので、 r とおけば、 πr 3 を導出できます。
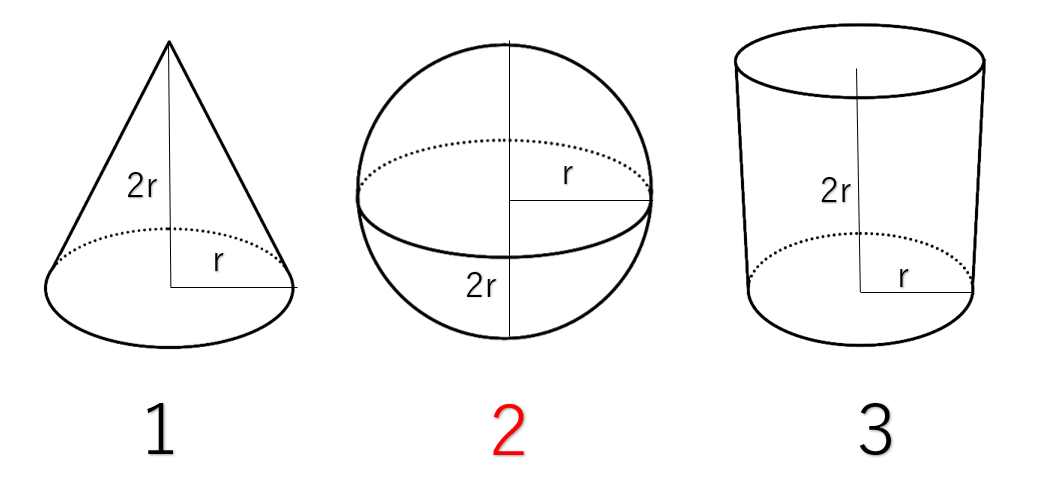
角錐・円錐の体積を問う問題は頻繁に出されます。 一方で円錐に比べると、球の体積を出す公式は重要ではありません。 ただ忘れてしまったとしても、以下の関係にあることを覚えておけば球の公式を作ることができます。 円錐:球:円柱=1:2:3 円柱に1/3を掛けることで、円錐の体積になります。 このとき、 円錐の体積の2倍が球です。 また、円柱の体積に 球の体積の求め方公式 半径 の球の体積を とすると、球の体積 は、次の公式で求められます。 (例題)半径5cmの球の体積を求めましょう。 求める球の体積を 、半径を とすると より 円錐:球:円柱=1:2:3 美しいですね。数の神秘を感じます。 ですので、球の体積の求め方は、円柱の体積の求め方に2/3をかけたらいいのです。 円柱の体積は 半径×半径×π×高さ ですので、ここでは、 r×r×π×2r=2πr 3 ですので球の体積は、 2πr 3 ×2/3= 4/3πr 3
球 体積 表面積 求め方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  | |
 |  |  |
「球 体積 表面積 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「球 体積 表面積 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「球 体積 表面積 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「球 体積 表面積 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 | ||
「球 体積 表面積 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「球 体積 表面積 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「球 体積 表面積 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「球 体積 表面積 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「球 体積 表面積 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 | ||
「球 体積 表面積 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「球 体積 表面積 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |
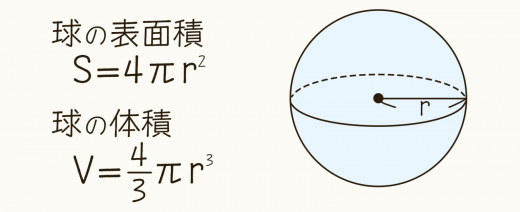
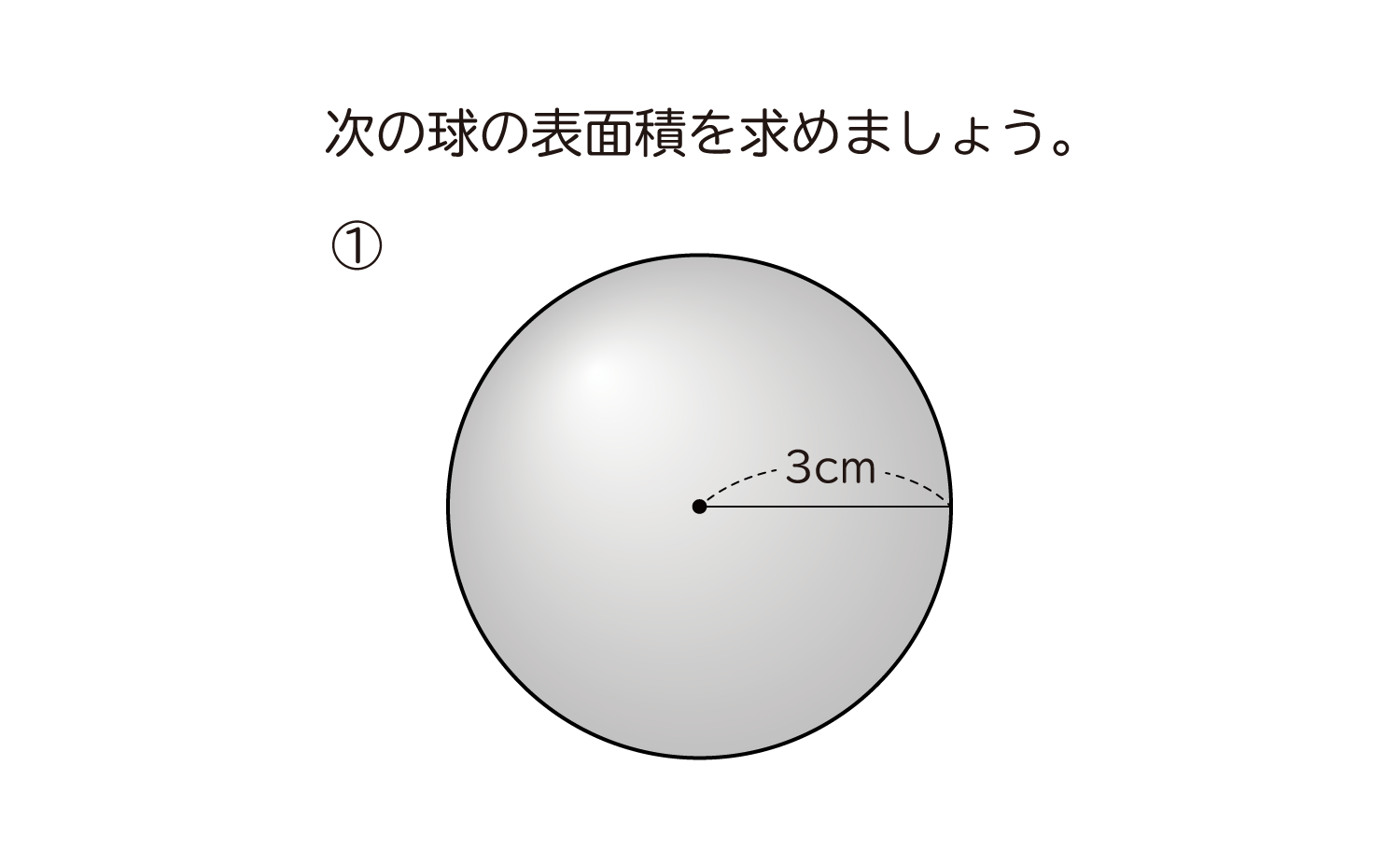
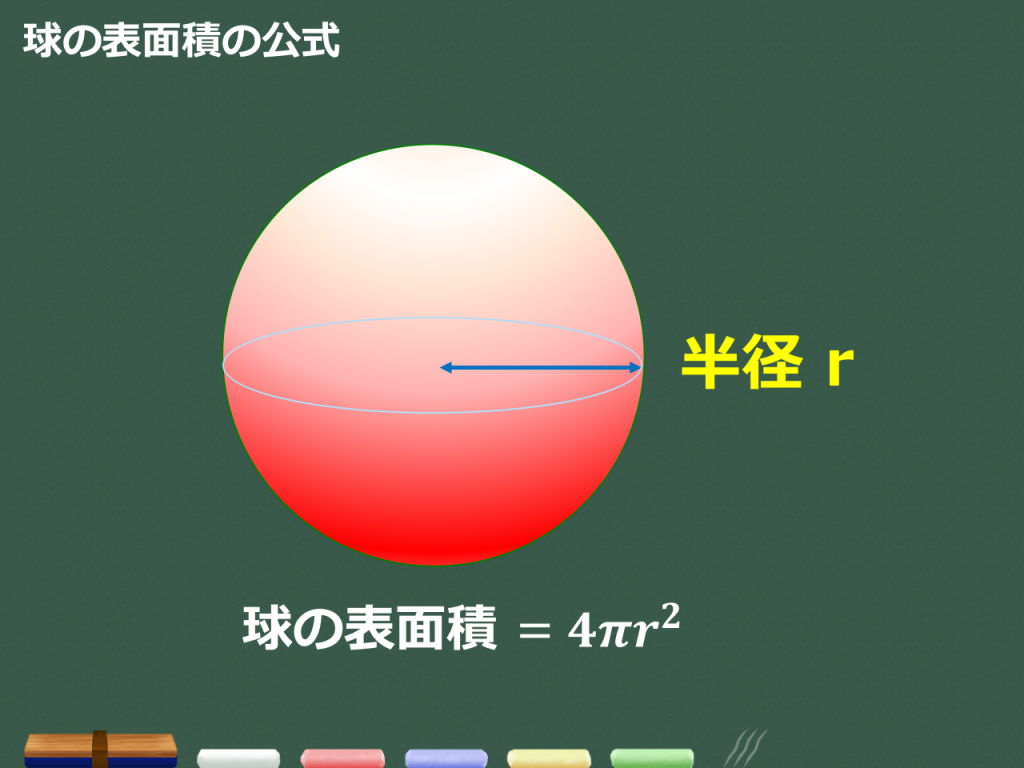
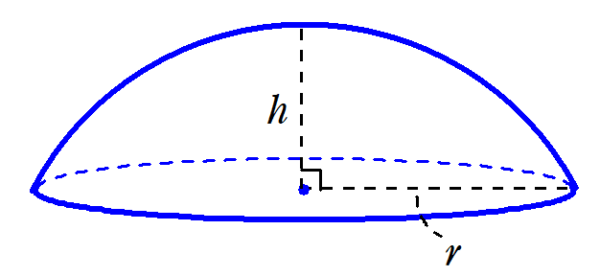
S = 4 π × 3 2 = 36 π S = 4 \pi \times 3^2 = 36\pi S = 4π × 32 = 36π 半球の表面積は,「この半分」と「半径 3 cm 3 \text { cm} 3 cm の円の面積」を足したものなので, 36 π π × 3 2 = 45 π 36\pi \pi \times 3^2 = 45\pi 36π π × 32 = 45π よって答えはまずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半径をr、円周率をπ、求める球の体積をVとすると これが球の体積を求める公式です。 ※2つとも公式ですので覚えるようにしましょう。 公式を覚えたら次ページの練習問題にチャレンジ!
Incoming Term: 球 体積 求め方, 球 体積 求め方 なぜ, 球 体積 求め方 積分, 球 体積 求め方 公式, 球 体積 表面積 求め方, 球 一部 体積 求め方, 数学 球 体積 求め方,
コメント
コメントを投稿